Overview:
This is an explanatory model of liquid diffusion in multi-solvent systems to assist in crystal discovery for the Robot-Accelerated Perovskite Investigation and Discovery (RAPID-2) project in the computational chemistry lab of Dr. Joshua Schrier. This model is written in MATLAB using a finite volume approximation of Fick’s second law of diffusion as a basis for liquid movement. I implement a non-linear optimization of input parameters to fit the model to experimental data, allowing us to determine solvent concentration profiles at the point of crystallization. With these profiles, we can expedite the discovery of perovskite organohalides by emulating a 96-well plate within a single solution and create predictive measures for solvent-systems with a high chance of crystallization
Write Up:
For an in depth understanding of this model, please see my write up below. This is an excerpt from our group’s paper “A spatiotemporal route to understanding metal halide perovskite crystallization” which is in preparation for submission to Chemistry of Materials.
RK_ModelforwebsiteExperiment Workflow:
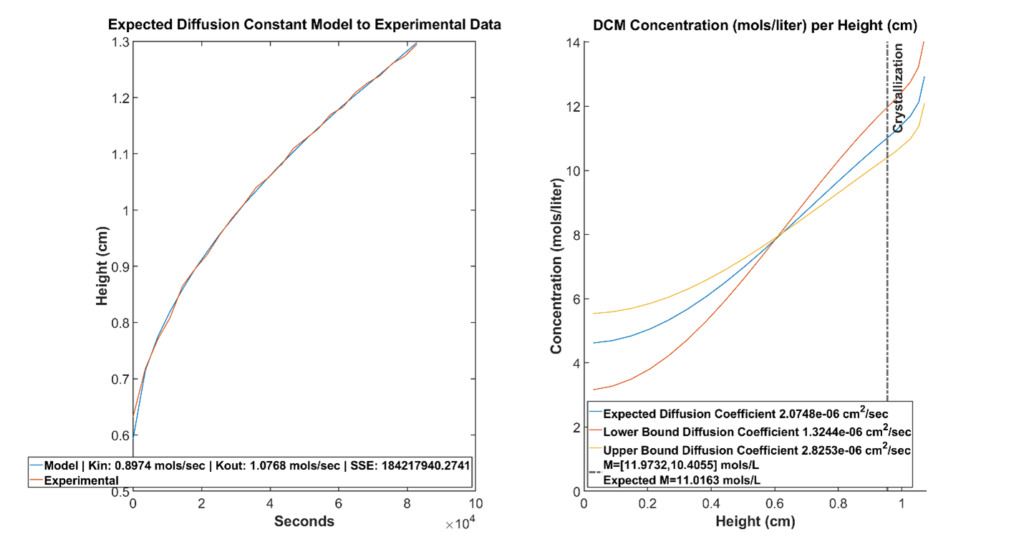
An experiment resulting in crystallization is run. The starting concentration of the mother liquor is recorded. The height build up of the solution resulting from antisolvent condensation over time is recorded.

Optimization:
The evaporation and condensation rate of antisolvent are determined by fitting the height build up calculated by the model to the experimental height build up.
Query Model:
After the optimization has determined the evaporation and condensation rates, the model is run again with these parameters.
Profit!
Finally, given the location and time of crystallization, we can query the model to determine the concentration profile of the solution at that point in time. The model also calculates an upper and lower bound determined by the experimental diffusion coefficient.